Você não pode entender algo a menos que você possa construir isso, esse é o nosso lema para essa série sobre os modelos de machine learning from scratch, ou seja, aprendendo do quase zero para sair da superfície e entender além do sklearn, no post anterior falamos sobre o KNN, sugiro que também dê uma conferida.
O Support Vector Machine (SVM) ou máquinas de vetores de suporte é um dos modelos de machine learning mais conhecidos e versáteis, utilizado tanto para tarefas de classificação quanto de regressão. Criado na década de 1990, o SVM continua a ser um modelo altamente eficaz, especialmente em situações onde a relação entre as variáveis não é linear.
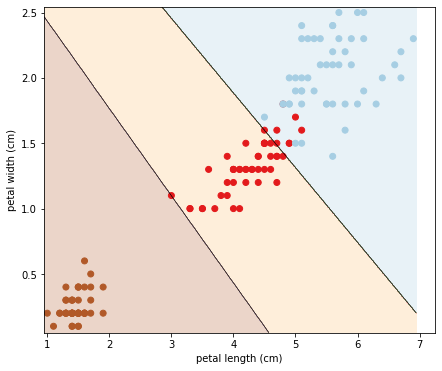
Tipo de aprendizado: Baseado em instância
Modelos baseados em instância, como o SVM, não aprendem uma função generalizada para todo o conjunto de dados, mas focam em separar as amostras de treinamento de maneira ótima. O SVM faz isso ao encontrar um hiperplano que melhor separa as classes no espaço de entrada. Ele seleciona um subconjunto dos dados de treinamento, os chamados vetores de suporte, que são essenciais para definir a fronteira de decisão. Esses vetores de suporte representam as instâncias mais desafiadoras para separar, e o modelo utiliza esses exemplos para maximizar a margem de separação entre as classes.
Como o SVM funciona
Passo 1: Definindo o Hiperplano
O SVM começa identificando um hiperplano que separa as classes de maneira ótima. Em um espaço bidimensional (2D), esse hiperplano é uma linha reta, mas em espaços de maior dimensão, ele se torna uma superfície de dimensão inferior (por exemplo, um plano em 3D). O objetivo é encontrar o hiperplano que maximiza a margem entre as classes, ou seja, a distância entre os pontos de dados mais próximos de cada classe e o hiperplano.
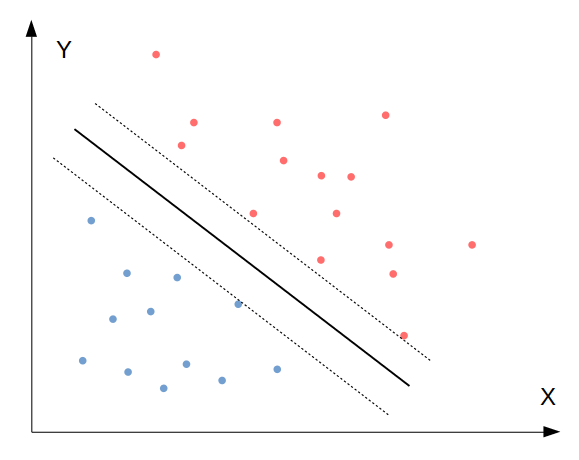
Passo 2: Maximização da Margem
Uma característica importante do SVM é a maximização da margem. A margem é a distância entre o hiperplano e os pontos de dados mais próximos, chamados de vetores de suporte. O SVM procura o hiperplano que maximiza essa margem, pois uma margem maior geralmente leva a uma melhor generalização do modelo, ou seja, ele funcionará melhor em dados que não foram usados no treinamento.
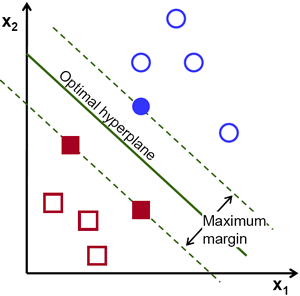
Matematicamente, a maximização da margem é formulada como um problema de otimização, onde o SVM tenta minimizar uma função de perda que leva em consideração tanto a margem quanto os erros de classificação (para casos em que os dados não são linearmente separáveis).
Passo 3: Tratando casos não linearmente separáveis
Nem sempre os dados podem ser separados linearmente. Nesses casos, o SVM utiliza o truque do kernel. Os kernels são funções que mapeiam os dados de entrada para um espaço de dimensão mais alta, onde uma separação linear se torna possível. Por exemplo, um kernel polinomial ou um kernel gaussiano (RBF) pode transformar um conjunto de dados que é inseparável em 2D em um conjunto separável em um espaço de maior dimensão.

Dessa forma, mesmo que as classes não possam ser separadas por uma linha reta no espaço original, elas podem ser separadas em um espaço transformado, permitindo que o SVM encontre um hiperplano linear naquele espaço.
Passo 4: Identificando os vetores de suporte
Os vetores de suporte são os pontos de dados que estão mais próximos do hiperplano e, portanto, são mais difíceis de classificar. Esses pontos são determinantes porque definem a posição do hiperplano. O SVM ajusta a posição do hiperplano com base nesses pontos, garantindo que a margem seja maximizada e que o modelo tenha a maior separação possível entre as classes.
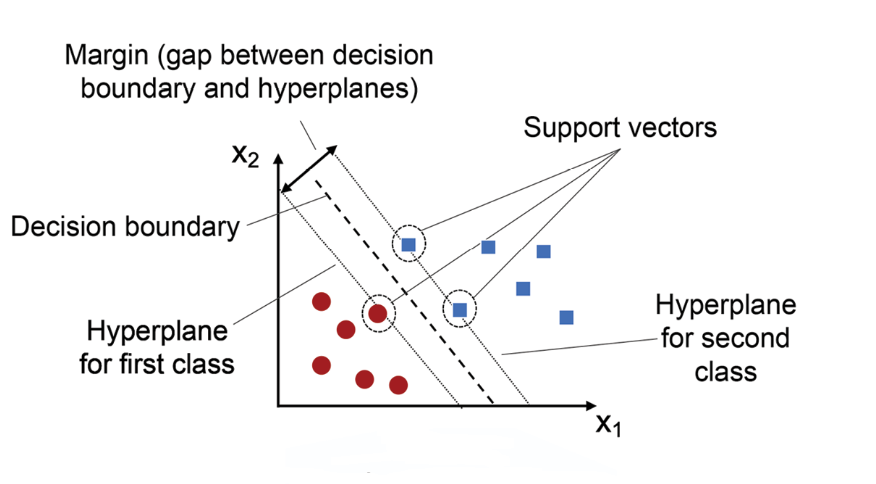
Passo 5: Classificação de novos dados
Uma vez que o SVM identificou o hiperplano ótimo e os vetores de suporte, ele está pronto para classificar novos dados. Para classificar uma nova amostra, o SVM simplesmente verifica de que lado do hiperplano essa amostra cai. Dependendo de qual lado a amostra está, o SVM a classifica em uma das classes.
Passo 6: Regularização e controle de erros
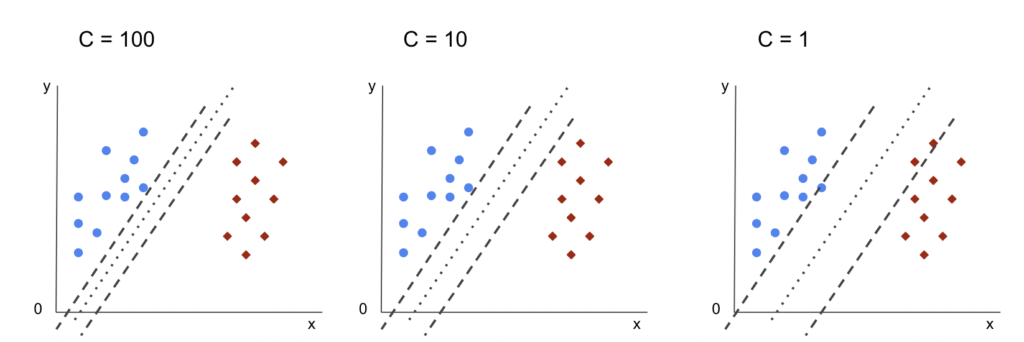
Em problemas onde os dados de treinamento podem ter ruído ou sobreposição entre classes, o SVM inclui um parâmetro de regularização C que controla a trade-off entre maximizar a margem e minimizar os erros de classificação. Um valor alto de C significa que o modelo tentará classificar corretamente a maior parte dos pontos de dados de treinamento, mesmo que isso resulte em uma margem menor. Um valor baixo de C, por outro lado, permitirá mais erros de classificação, mas com uma margem maior, o que pode melhorar a generalização do modelo.
Benefícios e aplicações do SVM
O Support Vector Machine (SVM) oferece uma série de benefícios que o tornam uma escolha popular em muitos problemas de machine learning. Além disso, suas aplicações abrangem diversas áreas e tipos de dados. Vamos explorar os principais benefícios e algumas das aplicações mais comuns do SVM.
Benefícios do SVM
- Eficaz em altas dimensões:
- O SVM é especialmente poderoso em situações onde os dados possuem muitas características (alta dimensionalidade). Devido à sua abordagem baseada em instância e uso de vetores de suporte, o SVM pode lidar eficientemente com espaços de grande dimensão, muitas vezes melhor que outros algoritmos.
- Utilização do truque do kernel:
- O uso de kernels permite que o SVM resolva problemas complexos de classificação, mesmo quando as classes não são linearmente separáveis no espaço original. Com kernels como o polinomial, RBF (Radial Basis Function), e sigmoid, o SVM pode mapear os dados para um espaço de maior dimensão onde a separação linear é possível.
- Margem máxima para melhor generalização:
- Ao maximizar a margem entre as classes, o SVM tende a generalizar melhor para dados novos, reduzindo o risco de overfitting (ajuste excessivo aos dados de treinamento). Isso é particularmente útil em datasets com um número limitado de exemplos.
- Flexibilidade com a regularização:
- O parâmetro de regularização C permite um controle fino sobre a complexidade do modelo. Ele possibilita ajustar o modelo para encontrar um equilíbrio entre uma margem ampla (que pode levar a erros) e uma margem mais estreita (que pode levar a overfitting).
- Robustez contra outliers:
- Devido ao foco nos vetores de suporte, o SVM é menos influenciado por outliers, especialmente quando o valor de C é ajustado adequadamente, o que permite ao modelo ignorar exemplos que estão muito longe das classes principais.
Aplicações do SVM
- Classificação de imagens: Como na identificação de dígitos manuscritos ou na categorização de objetos em imagens.
- Reconhecimento de padrões: Na biometria (reconhecimento facial, identificação de impressões digitais), se beneficiam da capacidade do SVM de separar classes complexas.
- Análise de sentimentos e Text mining: Pode ser utilizado para categorizar textos, e-mails, ou mesmo tweets em classes distintas (positivas, negativas, neutras), especialmente quando o espaço de características é grande (como em representações de texto).
- Bioinformática: Para classificar sequências de DNA, prever estruturas de proteínas e identificar genes de interesse.
- Detecção de fraude: Na identificação de transações fraudulentas, usam SVM para separar comportamentos normais de anômalos, graças à sua precisão e robustez em encontrar padrões em dados complexos.
O SVM se destaca por sua eficácia em cenários de alta dimensionalidade e pela flexibilidade que oferece através do uso de kernels e regularização. Suas aplicações são vastas, abrangendo desde a classificação de imagens até o diagnóstico médico, mostrando-se uma ferramenta eficaz e versátil para uma ampla gama de problemas de machine learning.
Implementação from scratch do SVM em Python
1. Importação das Bibliotecas
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
2. Dados de Treinamento
# Carrega os dados do dataset iris
iris = datasets.load_iris()
X = iris.data[:, :2] # Apenas duas features
y = iris.target
# Transformando em um problema binário
y = np.where(y == 0, -1, 1)
- No X estamos usando apenas 2 de 4 características do dataset Iris
- No y vamos definir duas classes (Iris Setosa vs. Não-Iris Setosa)
Essas modificações servem para facilitar a nossa explicação e visualização, mas você pode simular com todas as características caso queira.
# Plot dos dados
plt.figure()
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, edgecolor='k')
plt.show()
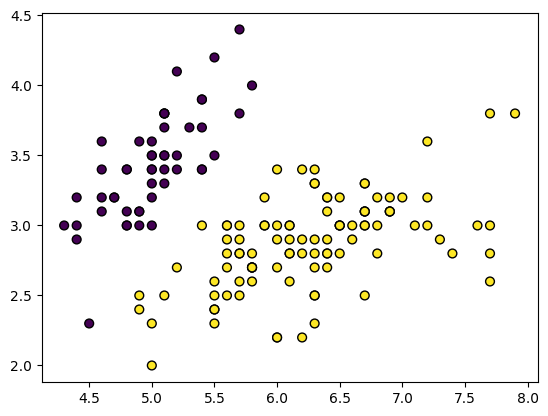
3. Dividindo os dados em treino e teste
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
4. Definindo a Classe SVM
A classe SVM (Support Vector Machine) implementa um modelo de aprendizado supervisionado usado para classificação de dados. O objetivo principal do SVM é encontrar a hiperplano de separação que maximiza a margem entre diferentes classes de amostras. Essa classe implementa a lógica do SVM passo a passo, incluindo o ajuste dos parâmetros durante o treinamento e a função de predição.
class SVM:
def __init__(self, learning_rate=0.001, lambda_param=0.01, n_iters=1000):
self.lr = learning_rate
self.lambda_param = lambda_param
self.n_iters = n_iters
self.w = None
self.b = None
def fit(self, X, y):
n_samples, n_features = X.shape
y_ = np.where(y <= 0, -1, 1)
self.w = np.zeros(n_features)
self.b = 0
for _ in range(self.n_iters):
for idx, x_i in enumerate(X):
condition = y_[idx] * (np.dot(x_i, self.w) - self.b) >= 1
if condition:
self.w -= self.lr * (2 * self.lambda_param * self.w)
else:
self.w -= self.lr * (2 * self.lambda_param * self.w - np.dot(x_i, y_[idx]))
self.b -= self.lr * y_[idx]
def predict(self, X):
approx = np.dot(X, self.w) - self.b
return np.sign(approx)
Vamos entender por partes:
def __init__(self, learning_rate=0.001, lambda_param=0.01, n_iters=1000):
self.lr = learning_rate
self.lambda_param = lambda_param
self.n_iters = n_iters
self.w = None
self.b = None
__init__: Inicializa os parâmetros do modelo, como a taxa de aprendizado, o parâmetro de regularização e o número de iterações.
n_iters = 1000 # número de iterações
self.lr = 0.001 # taxa de aprendizado
lambda_param = 0.01 #parâmetro de regularização da penalização
self.w = None # Inicialização da variável de pesos
self.b = None # Inicialização da variável de bias
def fit(self, X, y):
n_samples, n_features = X.shape
y_ = np.where(y <= 0, -1, 1)
self.w = np.zeros(n_features)
self.b = 0
fit: Ajusta os pesos (w) e o bias (b) para maximizar a margem entre as classes. Cada amostra é verificada e os pesos são atualizados conforme necessário.
n_samples, n_features = X_train.shape
# n_samples=120; n_features=2
y_ = np.where(y_train <= 0, -1, 1) # Converte labels para -1 e 1
w = np.zeros(n_features) # Cria um array para armazenar os pesos
b = 0 # bias
Loop para ajuste dos parâmetros do modelo (pesos w e bias b)
O objetivo desta função é maximizar a margem entre as classes, penalizando amostras que estejam violando essa margem, com o objetivo final de encontrar uma fronteira de decisão que separa as classes de forma otimizada.
for _ in range(self.n_iters):
for idx, x_i in enumerate(X):
condition = y_[idx] * (np.dot(x_i, self.w) - self.b) >= 1
if condition:
self.w -= self.lr * (2 * self.lambda_param * self.w)
else:
self.w -= self.lr * (2 * self.lambda_param * self.w - np.dot(x_i, y_[idx]))
self.b -= self.lr * y_[idx]
Vamos entender cada parte do loop:
for _ in range(self.n_iters):
Este loop externo percorre o número de iterações (n_iters) especificado. Cada iteração representa um ciclo de treinamento em que o modelo ajusta seus parâmetros (w e b) para melhorar a separação entre as classes.
for idx, x_i in enumerate(X):
Este loop interno percorre todas as amostras de treino (X). Para cada amostra, calculamos se ela está corretamente classificada ou se precisa de ajustes.enumerate(X): Retorna tanto o índice (idx) quanto a amostra (x_i). idx é usado para acessar o label correspondente em y_, enquanto x_i é a amostra atual em si.
condition = y_[idx] * (np.dot(x_i, self.w) - self.b) >= 1
Esta linha verifica se a amostra atual (x_i) está corretamente classificada e se não viola a margem máxima.
Cálculo:
np.dot(x_i, self.w): Calcula o produto escalar entre a amostrax_ie os pesosw, que corresponde à projeção da amostra nos pesos atuais.- self.b: Subtrai o bias (b), que ajuda a ajustar a fronteira de decisão.y_[idx] * (...): Multiplica o resultado da projeção pelo labely_[idx]. Se a amostra estiver corretamente classificada, o valor do produto deve ser maior ou igual a 1, atendendo à condição de margem máxima.
condition: A variável condition será True se a amostra estiver corretamente classificada e False se não estiver.
if condition:
self.w -= self.lr * (2 * self.lambda_param * self.w)
Se a condição for True, significa que a amostra x_i está corretamente classificada e não precisamos penalizar essa amostra, mas ainda precisamos aplicar uma pequena regularização.
Regularização:
2 * self.lambda_param * self.w: Este termo é uma penalização para evitar que os pesos cresçam demais, controlando o overfitting.lambda_paramé o parâmetro de regularização que determina a intensidade dessa penalização.- self.
lr * (...): Multiplica pela taxa de aprendizado (lr), que controla o tamanho do passo de ajuste dos pesos. - self.
w -= ...: Atualiza os pesos, diminuindo-os levemente para garantir que não fiquem excessivamente grandes.
else:
self.w -= self.lr * (2 * self.lambda_param * self.w - np.dot(x_i, y_[idx]))
self.b -= self.lr * y_[idx]
Se a condição for False, significa que a amostra x_i está violando a margem, e precisamos penalizar essa amostra, ajustando tanto os pesos w quanto o bias b.
Atualização dos Pesos:
2 * self.lambda_param * self.w: Termo de regularização como descrito anteriormente.np.dot(x_i, y_[idx]): Este termo penaliza a amostra mal classificada ajustando os pesos na direção correta para minimizar o erro. O valor denp.dot(x_i, y_[idx])é subtraído, aumentando ou diminuindowdependendo de como a amostra foi classificada.- self.
w -= ...: Atualiza os pesos levando em consideração tanto a regularização quanto o erro de classificação.
Atualização do Bias:
- self.
b -= self.lr * y_[idx]: Ajusta o biasbde acordo com o erro de classificação. Se a amostra foi mal classificada, o bias é ajustado para melhorar a classificação dessa e de outras amostras similares.
Ao imprimir a saída de 10 iterações para o terceiro item de X_train, temos:
Checking idx: 2
Classe incorreta, peso W após atualização: [ 1.04878727 -1.90865944]
Checking idx: 2
Classe incorreta, peso W após atualização: [ 0.98157752 -1.93927771]
Checking idx: 2
Classe incorreta, peso W após atualização: [ 0.9143812 -1.96988985]
Checking idx: 2
Classe incorreta, peso W após atualização: [ 0.84719833 -2.00049588]
Checking idx: 2
Classe incorreta, peso W após atualização: [ 0.78002889 -2.03109578]
Checking idx: 2
Classe correta, peso W após atualização: [ 0.77987288 -2.03068956]
Checking idx: 2
Classe correta, peso W após atualização: [ 0.77971691 -2.03028342]
Checking idx: 2
Classe correta, peso W após atualização: [ 0.77956096 -2.02987736]
Checking idx: 2
Classe correta, peso W após atualização: [ 0.77940505 -2.02947139]
Checking idx: 2
Classe correta, peso W após atualização: [ 0.77924917 -2.02906549]5. Função de predição
A função predict pega um conjunto de dados de entrada X, calcula sua posição relativa à fronteira de decisão do modelo usando um produto escalar com os pesos w e o bias b, e então converte essa posição em uma previsão de classe usando np.sign. Assim, ela retorna 1 ou -1 para cada amostra, indicando a classe prevista pelo modelo.
def predict(self, X):
approx = np.dot(X, self.w) - self.b
return np.sign(approx)
Vamos entender:
approx = np.dot(X, w) - self.b
Calcular a aproximação linear para cada amostra em X, que será usada para determinar em qual lado da fronteira de decisão a amostra se encontra.
Cálculo:
np.dot(X, self.w): Calcula o produto escalar entre cada amostra emXe os pesoswdo modelo. SeXtemnamostras emfeatures,Xserá uma matriz de dimensão(n, m)ewserá um vetor de dimensão(m,). O resultado denp.dot(X, self.w)será um vetor de dimensão(n,), onde cada elemento representa a projeção da respectiva amostra nos pesos.- self.b: Subtrai o biasbde cada projeção. O bias ajusta a fronteira de decisão do modelo, deslocando-a para melhor separar as classes.- Resultado: A variável
approxcontém os valores calculados para cada amostra, indicando sua posição relativa em relação à fronteira de decisão.
Esssa é a impressão da predição para o item 3 de X_train
predict(X_train[2:3])
array([-1.]) # Iris setosa6. Vamos aplicar a função fit() para obtermos os pesos
svm = SVM()
svm.fit(X_train, y_train)
svm = SVM(): Instancia o modelo SVM.svm.fit(X_train, y_train): Treina o modelo no conjunto de dados de treino.
7. Fazendo previsões no conjunto de teste
predictions = svm.predict(X_test)
Ao imprimirmos as saídas das predições, temos:
[ 1. -1. 1. 1. 1. -1. 1. 1. 1. 1. 1. -1. -1. -1. -1. 1. 1. 1.
1. 1. -1. 1. -1. 1. 1. 1. 1. 1. -1. -1.]8. Calculando a acurácia
accuracy = np.mean(predictions == y_test)
print(f"Acurácia: {accuracy * 100:.2f}%")
Calcula a acurácia do modelo comparando as previsões com as verdadeiras classes do conjunto de teste.
9. Visualizando a Fronteira de Decisão
Vamos plotar a fronteira de decisão criada pelo SVM sobre o conjunto de dados. Isso nos ajuda a visualizar como o modelo separa as diferentes classes.
def plot_decision_boundary(X, y, model):
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
np.arange(y_min, y_max, 0.01))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, edgecolor='k')
plt.show()
plot_decision_boundary(X_test, y_test, svm)
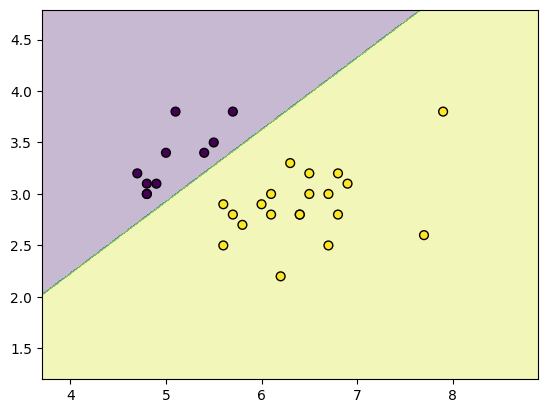
Conclusão
O Support Vector Machine (SVM) é um algoritmo de aprendizado de máquina versátil e eficaz para problemas de classificação, tanto linear quanto não linear. Ao determinar o hiperplano que maximiza a margem entre as classes, o SVM demonstra excelente desempenho em diversos cenários, especialmente quando a separabilidade das classes é bem definida. A implementação do SVM permite uma melhor compreensão dos seus mecanismos e oferece a flexibilidade de ajustar seus parâmetros para otimizar o modelo de acordo com as características específicas de cada conjunto de dados. Além disso, a utilização de kernels permite que o SVM lide com problemas não lineares, expandindo ainda mais seu campo de aplicação.
Recursos Adicionais
SVM em detalhes
Documentação oficial
Recomendação de livros: Recomendações




Pingback: Machine Learning from Scratch: Implementando K-Means Clustering em Python - IA Com Café