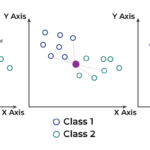
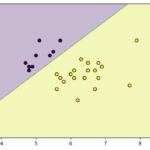
O clustering é uma das técnicas mais populares de aprendizado de máquina não supervisionado. Ele permite agrupar dados em diferentes categorias com base em similaridades. Entre os algoritmos de clustering, o K-Means é um dos mais amplamente utilizados devido à sua simplicidade e eficácia. Neste tutorial, vamos explorar como implementar o K-Means Clustering do zero em Python.
Ao final deste post, você entenderá os princípios teóricos do K-Means, como implementá-lo sem o uso de bibliotecas prontas e como aplicá-lo em um dataset real.
Também já implementamos o KNN e SVM, confere lá!

Teoria do K-Means clustering
O K-Means Clustering é um algoritmo iterativo que busca dividir os dados em K clusters. O objetivo é minimizar a soma das distâncias quadráticas entre os pontos de dados e o centroide do cluster ao qual pertencem.
Etapas do Algoritmo:
- Inicialização: Escolher K centros (centroides) iniciais aleatoriamente.
- Atribuição: Para cada ponto de dado, atribuir o cluster mais próximo com base na distância euclidiana.
- Atualização: Recalcular a posição dos centroides como a média dos pontos atribuídos a eles.
- Convergência: Repetir os passos 2 e 3 até que os centroides não mudem mais ou até que um número máximo de iterações seja atingido.
Conceitos matemáticos por trás do K-Means
O K-Means Clustering é um algoritmo que depende fortemente de conceitos matemáticos simples, mas poderoso. O primeiro deles é a distância, geralmente calculada usando a distância Euclidiana. Essa métrica mede o quão “próximos” dois pontos estão no espaço multidimensional. Para cada ponto no conjunto de dados, o K-Means calcula a distância entre ele e todos os centróides (os “centros” dos clusters) e atribui o ponto ao cluster cujo centróide está mais próximo. A fórmula da distância Euclidiana entre dois pontos: P(x1,y1) e Q(x2,y2)Q(x2,y2) é:
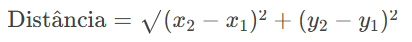
Outro conceito fundamental é a minimização da soma dos quadrados das distâncias (SSE – Sum of Squared Errors). O objetivo do K-Means é posicionar os centróides de forma que a soma das distâncias quadradas entre cada ponto e seu centróide seja a menor possível. Matematicamente, isso é representado por:
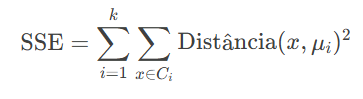
Onde k é o número de clusters, Ci é o conjunto de pontos no cluster i, e μi é o centróide do cluster i. O algoritmo itera entre dois passos principais: atribuição (onde os pontos são associados ao centróide mais próximo) e atualização (onde os centróides são recalculados como a média dos pontos em seu cluster). Esse processo continua até que os centróides não mudem significativamente, indicando que o algoritmo convergiu.
Desafios e limitações do K-Means
Apesar de ser um algoritmo poderoso e amplamente utilizado, o K-Means Clustering tem algumas limitações que é importante conhecer. Uma delas é a necessidade de definir o número de clusters (k) antecipadamente. Escolher um valor inadequado pode levar a resultados ruins, e métodos como o Elbow Method ou o Silhouette Score são frequentemente usados para ajudar nessa decisão. Outro desafio é a sensibilidade à inicialização dos centróides. Como o K-Means começa com centróides aleatórios, diferentes execuções podem levar a resultados diferentes, especialmente se os dados não estiverem bem distribuídos.
Além disso, o K-Means assume que os clusters são esféricos e de tamanho similar, o que nem sempre reflete a realidade. Dados com clusters de formatos irregulares ou densidades variadas podem ser mal representados pelo algoritmo. Outra limitação é a dificuldade em lidar com outliers (pontos fora do padrão), que podem distorcer a posição dos centróides. Por fim, o K-Means não funciona bem com dados categóricos, já que o cálculo de distâncias é baseado em valores numéricos. Essas limitações não tornam o K-Means menos útil, mas mostram a importância de entender o contexto dos dados e, quando necessário, considerar alternativas como DBSCAN ou clustering hierárquico.
Implementação do K-Means do zero
Aqui, implementaremos o algoritmo K-Means passo a passo. Para simplicidade, utilizaremos a distância euclidiana como métrica de similaridade.
1. Importação de bibliotecas
import numpy as np
import matplotlib.pyplot as plt
2. Inicialização dos centroides
Esta função é responsável por inicializar os centroides no algoritmo K-Means. Ele faz isso selecionando aleatoriamente K pontos do dataset para usar como centroides iniciais
def initialize_centroids(X, k):
"""Seleciona K pontos aleatórios do dataset como centroides iniciais."""
n_samples = X.shape[0]
random_indices = np.random.choice(n_samples, k, replace=False)
centroids = X[random_indices]
return centroids
3. Atribuição de clusters
Essa função é responsável pela atribuição de clusters no algoritmo K-Means. Ela calcula a distância de cada ponto até todos os centroides e atribui o ponto ao cluster mais próximo com base na menor distância. Isso é essencial para agrupar os dados em K clusters no K-Means.
def assign_clusters(X, centroids):
"""Atribui cada ponto ao cluster mais próximo."""
distances = np.linalg.norm(X[:, np.newaxis] - centroids, axis=2)
cluster_labels = np.argmin(distances, axis=1)
return cluster_labels
4. Atualização dos centroides
Esta função realiza a atualização dos centroides no algoritmo K-Means. Ela recalcula os centroides de cada cluster com a média dos pontos atribuídos ao respectivo cluster. Essa etapa é fundamental para ajustar os centroides, aproximando-os dos “centros” reais dos clusters formados pelos dados.
def update_centroids(X, cluster_labels, k):
"""Recalcula os centroides como a média dos pontos em cada cluster."""
new_centroids = np.array([X[cluster_labels == i].mean(axis=0) for i in range(k)])
return new_centroids
5. Algoritmo principal
Este bloco implementa o algoritmo principal do K-Means. Ele começa inicializando os centroides e, em seguida, itera através de duas etapas principais: atribuição de clusters e atualização dos centroides. O processo continua até atingir o número máximo de iterações (max_iters) ou até que os centroides converjam, ou seja, quando a mudança na posição de todos os centroides for menor que uma tolerância definida (tol). No final, o algoritmo retorna os centroides finais e os rótulos de cluster para os dados.
Essas etapas garantem que o algoritmo otimize a divisão dos dados em k grupos.
def kmeans(X, k, max_iters=100, tol=1e-4):
"""Executa o algoritmo K-Means."""
centroids = initialize_centroids(X, k)
for i in range(max_iters):
cluster_labels = assign_clusters(X, centroids)
new_centroids = update_centroids(X, cluster_labels, k)
# Verifica convergência
if np.all(np.abs(new_centroids - centroids) < tol):
break
centroids = new_centroids
return centroids, cluster_labels
Aplicando em um dataset real
Agora que temos nosso algoritmo, vamos aplicá-lo em um dataset real. Utilizaremos o famoso dataset Iris para simplificar.
6. Carregando e visualizando os dados
from sklearn.datasets import load_iris
# Carrega o dataset Iris
iris = load_iris()
X = iris.data[:, :2] # Apenas duas features para visualização
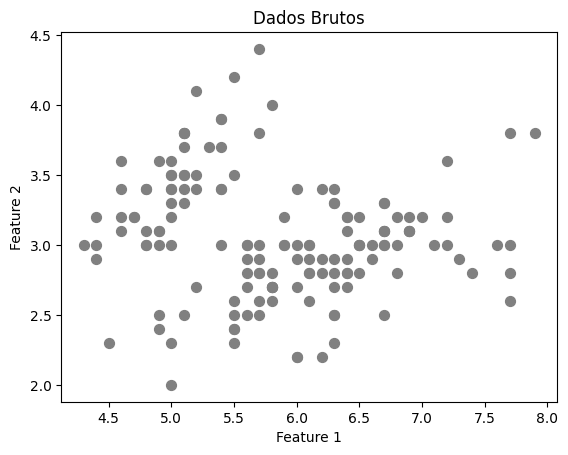
# Visualização inicial
plt.scatter(X[:, 0], X[:, 1], s=50, c='gray')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Dados Brutos')
plt.show()
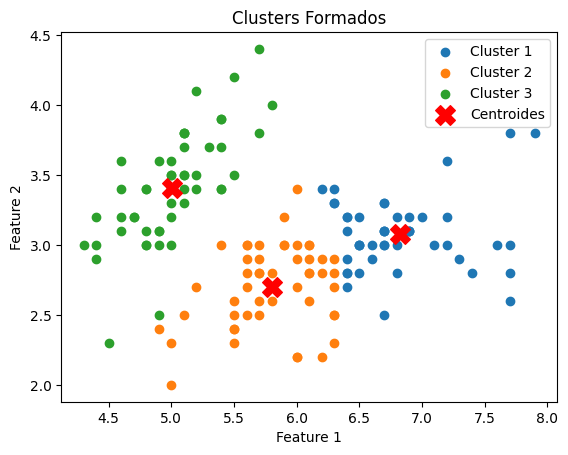
7. Executando o K-Means
Este bloco executa o algoritmo K-Means para dividir os dados em k clusters e, em seguida, visualiza os resultados.
k = 3 # Número de clusters
centroids, cluster_labels = kmeans(X, k)
# Visualização dos Clusters
for i in range(k):
plt.scatter(X[cluster_labels == i, 0], X[cluster_labels == i, 1], label=f'Cluster {i + 1}')
plt.scatter(centroids[:, 0], centroids[:, 1], s=200, c='red', marker='X', label='Centroides')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Clusters Formados')
plt.legend()
plt.show()
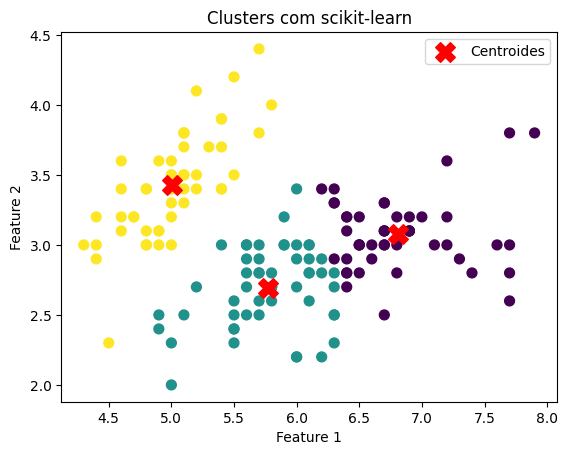
Comparando com scikit-learn
Para validar nossa implementação, comparemos com a versão do K-Means da biblioteca scikit-learn.
from sklearn.cluster import KMeans
kmeans_sklearn = KMeans(n_clusters=k, random_state=42)
kmeans_sklearn.fit(X)
# Visualização dos Clusters com scikit-learn
plt.scatter(X[:, 0], X[:, 1], c=kmeans_sklearn.labels_, cmap='viridis', s=50)
plt.scatter(kmeans_sklearn.cluster_centers_[:, 0], kmeans_sklearn.cluster_centers_[:, 1],
s=200, c='red', marker='X', label='Centroides')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Clusters com scikit-learn')
plt.legend()
plt.show()
Conclusão
Neste tutorial, implementamos o K-Means Clustering do zero, explorando desde a teoria até aplicações práticas. Também comparamos nossa solução com a implementação da scikit-learn, destacando a simplicidade e flexibilidade do algoritmo.
Agora é sua vez de experimentar! Teste o algoritmo com outros datasets e explore variações, como K-Means++ para inicialização inteligente dos centroides.
Deixe suas dúvidas ou experiências nos comentários. Até a próxima!
Recomendação de livros