A multicolinearidade é um problema silencioso que pode comprometer a interpretação dos modelos de machine learning e prejudicar suas previsões. Se você já construiu um modelo de regressão e percebeu que alguns coeficientes parecem instáveis ou sem sentido, pode estar lidando com esse problema.
Neste post, vamos entender o que é multicolinearidade, por que ela é prejudicial e como identificá-la e resolvê-la de maneira prática.

O que é Multicolinearidade?
A multicolinearidade ocorre quando duas ou mais variáveis independentes de um modelo estão altamente correlacionadas entre si. Isso significa que essas variáveis carregam informações redundantes, dificultando a identificação do impacto real de cada uma sobre a variável alvo.
Tipos de Multicolinearidade
- Multicolinearidade Perfeita: Quando uma variável pode ser expressa como uma combinação linear exata de outra(s). Exemplo: Se X3 = 2 * X1 + 3 * X2, há multicolinearidade perfeita.
- Multicolinearidade Imperfeita: Quando há uma forte correlação entre variáveis, mas não uma dependência exata.
Por que a Multicolinearidade é um Problema?
A presença de multicolinearidade pode gerar diversos problemas no seu modelo:
- Coeficientes Instáveis: Pequenas mudanças nos dados podem causar grandes variações nos coeficientes do modelo.
- Dificuldade na Interpretação: Como as variáveis são redundantes, fica difícil entender quais realmente influenciam o target.
- Overfitting: Modelos mais complexos, como regressões polinomiais, podem se ajustar demais aos dados de treino sem generalizar bem.
- Impacto na Seleção de Features: Algoritmos de seleção podem ser enganados e escolher variáveis erradas devido à redundância.
Exemplo Prático: O Problema na Predição de Preços de Casas
Imagine que você está construindo um modelo para prever o preço de uma casa (Preço), usando as variáveis:
- area_total (m²)
- area_construída (m²)
- numero_de_quartos
- numero_de_banheiros
Se area_total e area_construida forem altamente correlacionadas (o que é comum), o modelo pode ter dificuldades para determinar qual dessas variáveis impacta mais no preço. Isso tornaria os coeficientes instáveis e diminuiria a confiabilidade da análise.
Como Detectar a Multicolinearidade?
1. Matriz de Correlação
A maneira mais simples de identificar multicolinearidade é verificar a matriz de correlação entre as variáveis.
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# Exemplo de DataFrame com variáveis correlacionadas
dados = {
"area_total": [50, 60, 70, 80, 90],
"area_construida": [45, 55, 65, 75, 85],
"numero_de_quartos": [1, 2, 3, 3, 4],
"numero_de_banheiros": [1, 1, 2, 2, 3]
}
df = pd.DataFrame(dados)
# Matriz de correlação
plt.figure(figsize=(6,4))
sns.heatmap(df.corr(), annot=True, cmap="coolwarm", fmt=".2f")
plt.title("Matriz de Correlação")
plt.show()
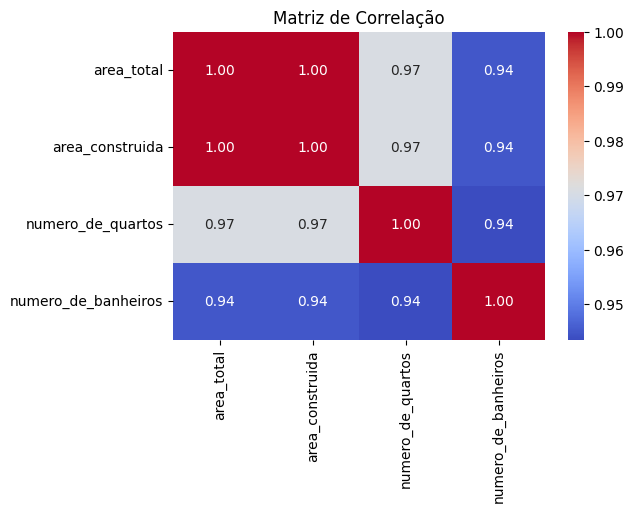
Se duas ou mais variáveis apresentarem correlações superiores a 0.8 ou -0.8, há um forte indício de multicolinearidade.
2. Variance Inflation Factor (VIF)
O VIF mede o quanto a variância de um coeficiente é aumentada devido à correlação com outras variáveis. Quanto maior o VIF, maior o impacto da multicolinearidade.
from statsmodels.stats.outliers_influence import variance_inflation_factor
import numpy as np
# Cálculo do VIF
X = df.drop(columns=["numero_de_banheiros"]) # Excluímos a variável alvo
vif_data = pd.DataFrame()
vif_data["variavel"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
print(vif_data)
variavel VIF
0 area_total 17442.000000
1 area_construida 20119.000000
2 numero_de_quartos 17.333333Valores de VIF acima de 5 ou 10 indicam forte multicolinearidade e exigem atenção.
Como Resolver a Multicolinearidade?
Se detectar multicolinearidade no seu modelo, aqui estão algumas formas de lidar com o problema:
1. Remover Variáveis Redundantes
Se duas variáveis carregam informações semelhantes, remova uma delas. No exemplo anterior, se area_total e area_construida forem muito correlacionadas, manter apenas uma pode ser uma boa estratégia.
2. Criar Novas Variáveis
Se as variáveis são correlacionadas mas individualmente importantes, tente criar uma variável derivada. Exemplo:
df["proporcao_area_construida"] = df["area_construida"] / df["area_total"]
df.drop(columns=["area_construida"], inplace=True)
3. Usar Modelos Menos Sensíveis à Multicolinearidade
Modelos baseados em árvores de decisão (como Random Forest e XGBoost) não são tão afetados pela multicolinearidade quanto regressões lineares.
4. Aplicar Regularização (Lasso e Ridge)
Técnicas como Ridge Regression (L2) ajudam a minimizar o impacto da multicolinearidade ao penalizar coeficientes excessivamente grandes.
from sklearn.linear_model import Ridge
modelo = Ridge(alpha=1.0) # Aumente alpha para uma penalização maior
modelo.fit(X, df["numero_de_banheiros"])
Conclusão
A multicolinearidade pode comprometer a estabilidade e interpretação de um modelo, mas com as técnicas corretas é possível identificar e mitigar seus efeitos.
Resumo das principais dicas:
- ✅ Sempre analise a matriz de correlação antes de treinar o modelo.
- ✅ Utilize o VIF para medir a intensidade do problema.
- ✅ Remova variáveis redundantes ou crie novas variáveis mais informativas.
- ✅ Modelos baseados em árvores são menos afetados por esse problema.
- ✅ Use regularização (Ridge/Lasso) para minimizar impactos.
Entender e resolver a multicolinearidade é essencial para construir modelos mais confiáveis e interpretáveis.
Gostou do conteúdo? Deixe seu comentário e compartilhe com quem precisa entender melhor esse problema!
Recomendação de livros para inpulsionar sua carreira
- Mãos à obra aprendizado de máquina com Scikit-Learn, Keras & TensorFlow: conceitos, ferramentas e técnicas para a construção de sistemas inteligentes.
- Python para análise de dados
- Estatística Prática Para Cientistas de Dados: 50 Conceitos Essenciais
- An Introduction to Statistical Learning (Python e R)




