No mundo do Machine Learning e da estatística, nos deparamos frequentemente com os termos “modelos paramétricos” e “modelos não paramétricos”. Entender a diferença entre eles é importante para escolher o modelo certo para um determinado problema. Ambos têm suas vantagens e limitações, vamos desmistificar os conceitos, mostrar exemplos e destacar suas aplicações práticas.

O que são Modelos Paramétricos?
Modelos paramétricos fazem suposições fortes sobre a forma da distribuição dos dados. Eles assumem que os dados podem ser representados por uma distribuição de probabilidade conhecida, como a distribuição normal (gaussiana), a distribuição binomial ou a distribuição de Poisson. Esses modelos são caracterizados por um número fixo de parâmetros que descrevem completamente a distribuição.
Características dos Modelos Paramétricos:
- Suposições sobre a distribuição: Assumem uma forma específica para a distribuição dos dados.
- Número fixo de parâmetros: São definidos por um conjunto fixo de parâmetros.
- Mais eficientes quando as suposições são válidas: Requerem menos dados para treinar e são computacionalmente mais rápidos quando as suposições sobre a distribuição são corretas.
- Sensíveis a violações das suposições: Se as suposições sobre a distribuição não forem válidas, o desempenho do modelo pode ser comprometido.
Exemplos de Modelos Paramétricos:
- Regressão Linear: Assume que a relação entre as variáveis independentes e a variável dependente é linear e que os erros seguem uma distribuição normal.
- Regressão Logística: Assume que a probabilidade de um evento ocorrer pode ser modelada por uma função logística.
- Análise Discriminante Linear (LDA): Assume que as classes têm distribuições gaussianas com a mesma matriz de covariância.
- Naive Bayes: Assume independência condicional entre as características, dado a classe.
O que são Modelos Não Paramétricos?
Modelos não paramétricos não fazem suposições fortes sobre a forma da distribuição dos dados. Eles são mais flexíveis e podem se adaptar a uma variedade maior de formas de distribuição. Em vez de um número fixo de parâmetros, a complexidade do modelo cresce com a quantidade de dados, eles se adaptam à complexidade do dataset, tornando-os mais flexíveis, especialmente em situações onde os dados têm padrões complexos ou desconhecidos.
Características dos Modelos Não Paramétricos:
- Menos suposições sobre a distribuição: Não assumem uma forma específica para a distribuição dos dados.
- Complexidade varia com os dados: A complexidade do modelo aumenta com a quantidade de dados.
- Mais flexíveis e robustos: Podem modelar relações complexas e são menos sensíveis a outliers e violações das suposições sobre a distribuição.
- Requerem mais dados para treinar: Geralmente precisam de mais dados para atingir um bom desempenho e podem ser computacionalmente mais intensivos.
Exemplos de Modelos Não Paramétricos:
- Árvores de Decisão (e Random Forests, Gradient Boosting): Particionam o espaço de características em regiões retangulares para fazer previsões.
- Máquinas de Vetores de Suporte (SVMs): Encontram um hiperplano que melhor separa as classes.
- Redes Neurais: Consistem em camadas de neurônios interconectados que aprendem representações complexas dos dados.
- k-Nearest Neighbors (k-NN): Classificam um novo ponto com base na classe dos seus k vizinhos mais próximos.
- Regressão Não Paramétrica (ex: Regressão Local): Estima a relação entre variáveis sem assumir uma forma funcional predefinida.
Comparação direta:
| Característica | Modelos Paramétricos | Modelos Não Paramétricos |
|---|---|---|
| Suposições | Fortes suposições sobre a distribuição dos dados | Poucas ou nenhuma suposição sobre a distribuição dos dados |
| Complexidade | Fixa, definida por um número fixo de parâmetros | Varia com a quantidade de dados |
| Eficiência | Mais eficientes quando as suposições são válidas | Menos eficientes em termos de dados e computação, geralmente |
| Flexibilidade | Menos flexíveis | Mais flexíveis |
| Robustez a outliers | Mais sensíveis a outliers e violações das suposições | Mais robustos a outliers e violações das suposições |
| Dados Necessários | Menos dados, geralmente | Mais dados, geralmente |
Quando usar qual tipo de modelo?
A escolha entre modelos paramétricos e não paramétricos depende do problema em questão e das características dos dados:
- Use modelos paramétricos quando:
- Você tem um bom entendimento da distribuição dos dados e pode fazer suposições razoáveis.
- Você tem uma quantidade limitada de dados.
- A eficiência computacional é uma preocupação importante.
- Use modelos não paramétricos quando:
- Você não tem conhecimento prévio sobre a distribuição dos dados.
- Os dados são complexos e não seguem uma distribuição conhecida.
- Você tem uma grande quantidade de dados disponíveis.
- A precisão é mais importante que a eficiência computacional.
Exemplo prático e didático: Prevendo a altura de pessoas
Imagine que temos os seguintes dados:
| Idade (anos) | Altura (cm) |
|---|---|
| 5 | 110 |
| 10 | 140 |
| 15 | 165 |
| 20 | 175 |
| 25 | 178 |
| 30 | 178 |
| 40 | 178 |
| 45 | 178 |
Queremos prever a altura de uma pessoa com base na idade. Vamos usar dois modelos:
- Paramétrico: Regressão Linear.
Assumiremos que existe uma relação linear entre idade e altura. - Não Paramétrico: K-Nearest Neighbors (KNN).
Permitiremos que o modelo encontre padrões diretamente nos dados, sem suposições.
Passo 1: Visualizando os Dados
Vamos plotar os pontos para entender o comportamento.
import numpy as np
import matplotlib.pyplot as plt
# Dados de exemplo
idade = np.array([5, 10, 15, 20, 25, 30, 40, 45])
altura = np.array([110, 140, 165, 175, 178, 178, 178, 178])
# Plot
plt.scatter(idade, altura, color='blue', label='Dados Observados')
plt.xlabel('Idade (anos)')
plt.ylabel('Altura (cm)')
plt.title('Altura vs Idade')
plt.legend()
plt.show()
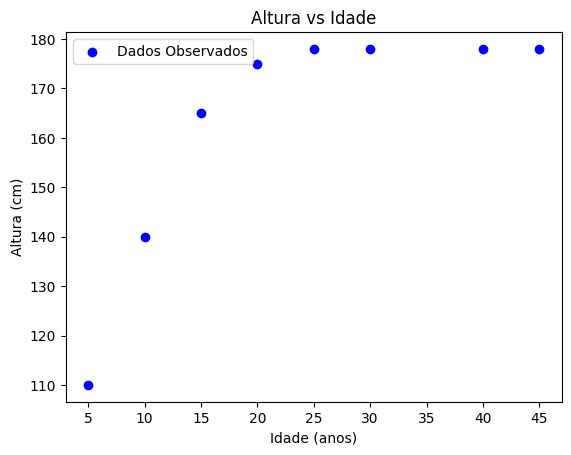
Esse gráfico mostra que a altura cresce rápido na infância, estabilizando-se na idade adulta.
Passo 2: Modelo Paramétrico (Regressão Linear)
A regressão linear ajustará uma linha reta aos dados, assumindo uma relação fixa.
from sklearn.linear_model import LinearRegression
# Regressão Linear
idade = idade.reshape(-1, 1) # Transformando para matriz
modelo_parametrico = LinearRegression()
modelo_parametrico.fit(idade, altura)
# Previsão
idade_teste = np.array([8, 18, 25, 30, 40, 45]).reshape(-1, 1) # Testando idades fora da amostra
previsoes_parametricas = modelo_parametrico.predict(idade_teste)
# Plot
plt.scatter(idade, altura, color='blue', label='Dados Observados')
plt.plot(idade, modelo_parametrico.predict(idade), color='red', label='Regressão Linear')
plt.scatter(idade_teste, previsoes_parametricas, color='green', label='Previsões')
plt.xlabel('Idade (anos)')
plt.ylabel('Altura (cm)')
plt.title('Modelo Paramétrico - Regressão Linear')
plt.legend()
plt.show()
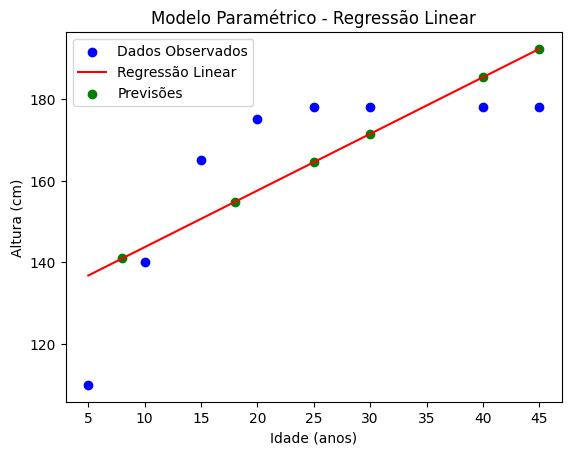
Resultados:
O modelo linear cria uma linha reta que tenta generalizar o comportamento dos dados. Porém, para idades muito altas (ex.: 30 anos), a previsão pode ser imprecisa porque o crescimento já estabilizou.
Passo 3: Modelo Não Paramétrico (KNN)
Com o KNN, o modelo usará as alturas dos vizinhos mais próximos para prever novas idades.
from sklearn.neighbors import KNeighborsRegressor
# KNN
modelo_nao_parametrico = KNeighborsRegressor(n_neighbors=2) # Usando 2 vizinhos
modelo_nao_parametrico.fit(idade, altura)
# Previsão
previsoes_nao_parametricas = modelo_nao_parametrico.predict(idade_teste)
# Plot
plt.scatter(idade, altura, color='blue', label='Dados Observados')
plt.scatter(idade_teste, previsoes_nao_parametricas, color='orange', label='Previsões')
plt.xlabel('Idade (anos)')
plt.ylabel('Altura (cm)')
plt.title('Modelo Não Paramétrico - KNN')
plt.legend()
plt.show()
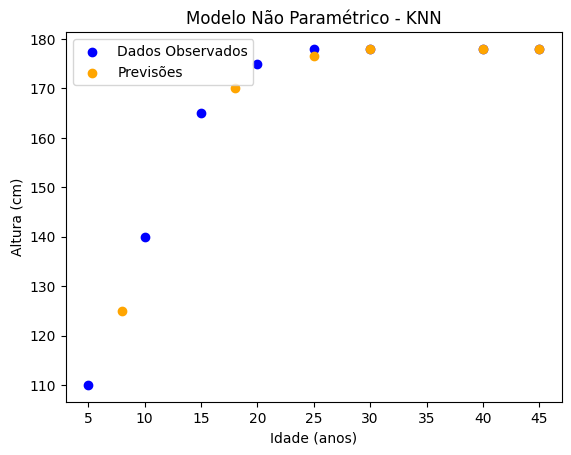
Resultados:
O KNN prevê a altura baseando-se nas idades mais próximas no dataset. Ele não assume nenhuma forma fixa e adapta-se melhor a padrões complexos, mas pode ser sensível a ruídos nos dados.
No exemplo, vimos que o modelo paramétrico (regressão linear) pode ser limitado ao lidar com padrões mais complexos (crescimento que desacelera com a idade). Já o modelo não paramétrico (KNN) adaptou-se melhor, mas requer mais dados para capturar o comportamento geral.
Conclusão
Tanto os modelos paramétricos quanto os não paramétricos têm seus pontos fortes e fracos. A compreensão das diferenças entre eles é necessária para escolher o modelo mais adequado para cada tarefa de Machine Learning ou análise estatística. Não existe uma “melhor” abordagem universal; a escolha depende do contexto específico do problema e das características dos dados disponíveis. Em muitos casos, a experimentação com diferentes tipos de modelos é a melhor maneira de determinar qual deles oferece o melhor desempenho.
Recomendação de livros
- Mãos à obra aprendizado de máquina com Scikit-Learn, Keras & TensorFlow: conceitos, ferramentas e técnicas para a construção de sistemas inteligentes.
- Python para análise de dados
- Estatística Prática Para Cientistas de Dados: 50 Conceitos Essenciais
- An Introduction to Statistical Learning (Python e R)




